FPGA定点和浮点数学运算实例对比
- 期货快讯
- 2025-07-09
- 31952
来源:OpenFPGA;作者:碎碎思
在创建 RTL 示例时,经常使用 VHDL 2008 附带的 VHDL 包。它提供了出色的功能,可以高效地处理定点数,当然,它们也是可综合的。该包的一些优点包括:
有符号和无符号(后缀和后缀)定点向量。
轻松将定点数表示并量化为定点向量。
小数点位于向量元素 0 和 -1 之间。这样就无需在运算过程中跟踪小数点以进行对齐(大量运算这点很难把握)。
运算的溢出、舍入和范围管理有明确的定义。
算术和比较运算符。
因此,当需要实现算法时,我会使用这个包。但是实际应用时,还会有很多浮点运算。
自然而然地,一个问题出现了:用定点和浮点实现同一个方程时,资源有什么区别?
我们将要看的例子是如何利用多项式近似地将ADC读数转换为温度值。这在工业应用中很常见(使用铂电阻温度计时)。
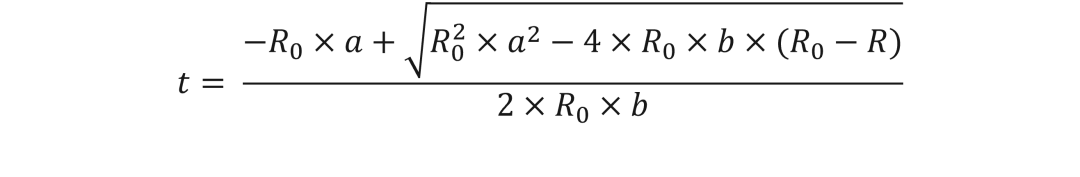
要实现的具体方程是 y = 2E-09x4 - 4E-07x3 + 0.011x2 + 2.403x - 251.26,该方程是从绘制方程式中提取出来的。虽然我们可以直接实现该方程,但这会非常浪费资源,还会增加开发的复杂性和风险。
使用定点数系统,我们需要做一些量化来保持精度和准确度。
代码和一个简单的仿真如下。
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use ieee.fixed_pkg.all;
entity complex_example is port(
clk :instd_logic;
ip :instd_logic_vector(7 downto 0);
op : out std_logic_vector(8 downto 0));
end complex_example;
architecture Behavioral of complex_example is
signal power_a : sfixed(8 downto -32):=(others=>'0');
signal power_b : sfixed(8 downto -32):=(others=>'0');
signal power_c : sfixed(8 downto -32):=(others=>'0');
signal calc : sfixed(8 downto -32) :=(others=>'0');
signal store : sfixed(8 downto 0) := (others =>'0');
constant a : sfixed(8 downto -32):= to_sfixed( 2.00E-09, 8,-32 );
constant b : sfixed(8 downto -32):= to_sfixed( 4.00E-07, 8,-32 );
constant c : sfixed(8 downto -32):= to_sfixed( 0.0011, 8,-32 );
constant d : sfixed(8 downto -32):= to_sfixed( 2.403, 8,-32 );
constant e : sfixed(8 downto -32):= to_sfixed( 251.26, 8,-32 );
typereg_array is array (9 downto 0) of sfixed(8 downto -32);
signal pipeline_reg : reg_array;
begin
cvd : process(clk)
begin
ifrising_edge(clk)then
store <= to_sfixed('0'&ip,store);
power_a <= resize (arg => power_b * store * a,
size_res => power_a);
power_b <= resize (arg => power_c * store * b,
size_res => power_b);
power_c <= resize (arg => store * store * c,
size_res => power_c);
calc <= resize (arg => power_a - power_b + power_c + (store * d) - e,
size_res => calc);
pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) & calc;
op <= to_slv(pipeline_reg(pipeline_reg'high)(8 downto 0));
end if;
end process;
end Behavioral;
对于 109 Ω的电阻输入,温度应报告为 23.7°C。我们可以在下面的定点仿真中看到,结果符合预期,精度在可接受的范围内。
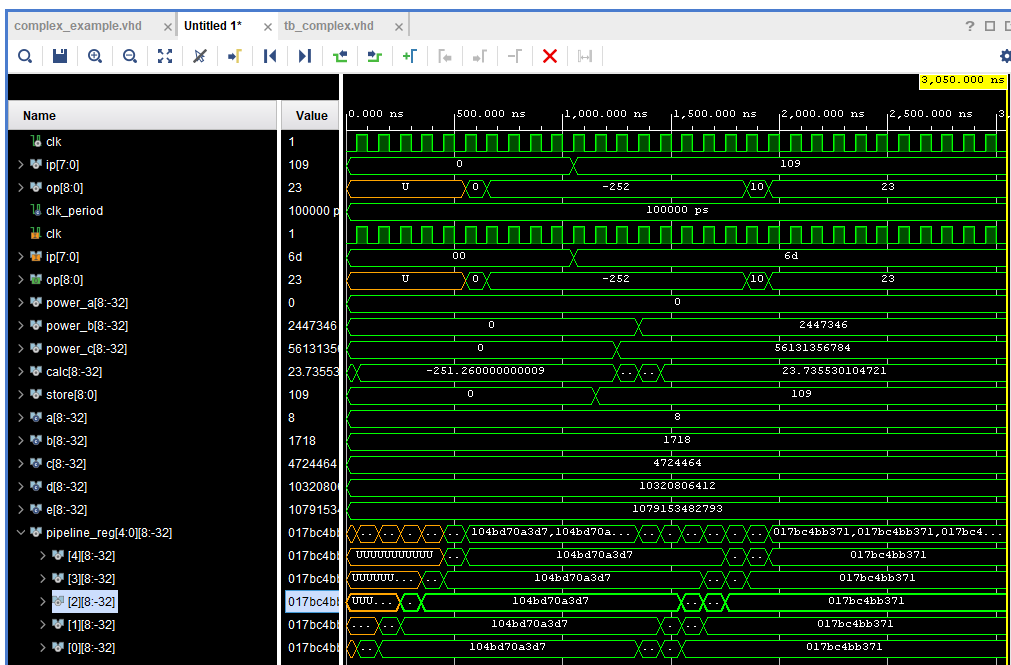
使用浮点包实现相同的功能,以类似的方式实现
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.FLOAT_pkg.ALL; -- Use the floating-point package
entity FloatingPointPolynomial is
Port (
clk :inSTD_LOGIC;
x :infloat32; -- Input x as a 32-bit floating-point number
y : out float32 -- Output y as a 32-bit floating-point number );
end FloatingPointPolynomial;
architecture Behavioral of FloatingPointPolynomial is
-- Define constantsforthe polynomial coefficients
constant a4 : float32 := TO_float(2.00E-09);
constant a3 : float32 := TO_float(-4.00E-07);
constant a2 : float32 := TO_float(0.011);
constant a1 : float32 := TO_float(2.403);
constant a0 : float32 := TO_float(-251.26);
signal x2, x3, x4 : float32; -- Intermediate powers of x
signal term4, term3, term2, term1 : float32; -- Polynomial terms
signal res : float32;
typereg_array is array (9 downto 0) of float32;
signal pipeline_reg : reg_array;
begin
process(clk)
begin
ifrising_edge(clk)then
-- Calculate powers of x
x2 <= x * x;
x3 <= x2 * x;
x4 <= x3 * x;
-- Calculate each term in the polynomial
term4 <= a4 * x4;
term3 <= a3 * x3;
term2 <= a2 * x2;
term1 <= a1 * x;
-- Calculate final result
res <= term4 + term3 + term2 + term1 + a0;
pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) &
res;
y <= (pipeline_reg(pipeline_reg'high));
end if;
end process;
end Behavioral;
仿真再次显示了预期的结果,作为浮点结果,我们得到的结果也包括分数元素。
因此,定点和浮点都能够实现定义的算法。
为了了解利用所需的资源,决定将这两种算数实现都以 K26 SoM 为目标进行综合。
运行综合将识别每个模块所需的资源。
正如预期的那样,定点实现所需的逻辑占用空间比浮点实现所需的小得多。
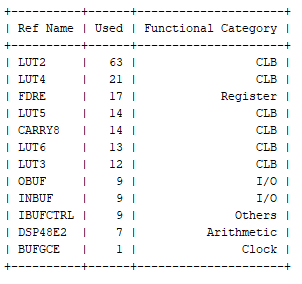
定点实现
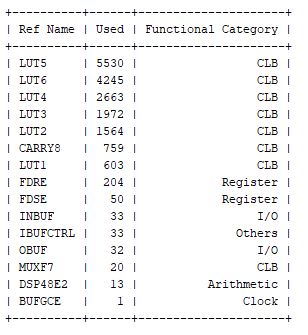
浮点实现
我们不仅需要考虑逻辑占用空间,还需要考虑时序性能。考虑到这一点,将两个设计都设置为 200 MHz 运行,并从一开始就实现了基准时序收敛。
实现时序收敛比定点收敛更重要,这在浮点实现中是可以预料到的。不得不重新审视设计,并在几个关键阶段实现流水线,因为最初的代码只是为了确定占用空间的差异。
值得注意的是,Versal 系列中的 DSP58 支持浮点运算,但它不能直接从 float32 映射到 DSP。为了利用此功能,我们需要实例化配置为 FP32 操作的 DSP58,或者利用 Vivado IP 集成器提供的浮点 IP。
总结这篇博客,正如预期的那样,在使用 VHDL 中的浮点库时,逻辑占用空间存在很大差异。
建议在必要时利用定点,并在绝对必要时限制浮点。